Продолжаем тему, начатую ранее. В этой части будут рассмотрены более сложные типы уравнений “квадрат сопоставлен корням и числу” и “квадрат и корни сопоставлены числу”. В обоих случаях уравнение имеет единственное положительное решение. Оба случая требуют геометрического построения квадратного корня (см. ранее описанный тип уравнения “квадрат сопоставлен числу”).
Квадрат сопоставлен корням и числу: х² = ах + m
Предварительно находятся длины отрезков а/2 и √m.
Построить прямой угол с вершиной О.
На одной стороне угла отложить отрезок ОА = а/2. На другой стороне угла отложить отрезок ОВ = √m.
Провести дугу окружности с центром в точке А и радиусом АВ до пересечения в точке С со стороной угла ОА.
Длина отрезка ОС является решением уравнения.
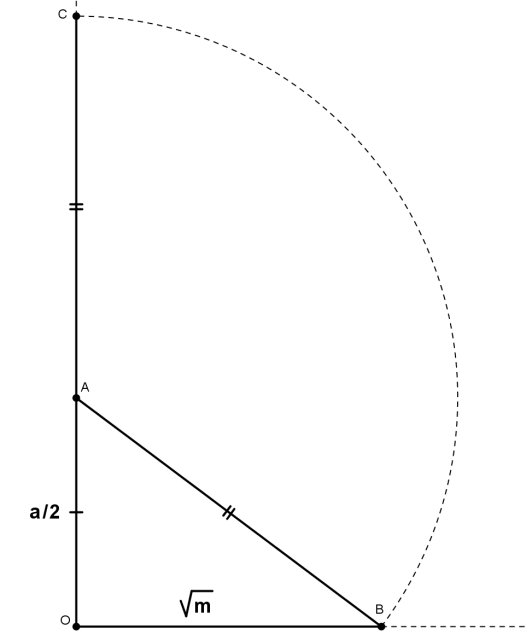
Квадрат и корни сопоставлены числу: х² + ах = m
Предварительно находятся длины отрезков а/2 и √m.
Построить прямой угол с вершиной О, продолжить одну из его сторон.
На продолженной стороне угла отложить отрезок ОА = а/2. На другой стороне угла отложить отрезок ОВ = √m.
Провести дугу окружности с центром в точке А и радиусом АВ до пересечения в точке С с продолжением стороны угла ОА (точка О должна лежать между точками С и А)“
Длина отрезка АС является решением уравнения.

Комментариев нет:
Отправить комментарий