Целые степени — циркулем и линейкой

Среди геометрических построений, о которых не рассказывают в школе, есть и такое, как нахождение целых степеней. Включая и отрицательные. Правда, у него есть и ограничение: основанием степени должно быть число, строго большее единицы. Этот способ упоминается во флорентийских трактатах XV века по строительству и когда-то широко использовался при разработке декоративных элементов.

Итак, пусть имеется некоторое число x>1. Требуется найти любую его целую степень, пользуясь только циркулем и линейкой.

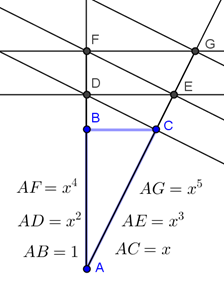
1. Построить прямоугольный треугольник АВС с прямым углом В, единичным катетом АВ=1 и гипотенузой АС=х. (Для этого строится прямой угол, на одной его стороне единичным раствором от вершины делается засечка А, затем от этой точки раствором х делается засечка С на другой стороне угла.)
2. Из точки А провести лучи, служащие продолжениями катета АВ и гипотенузы АС.
3. К лучу АС провести перпендикуляр через точку С до пересечения с другим лучом в точке D.
4. К лучу АВ через точку D провести перпендикуляр до пересечения с другим лучом в точке Е.
   
   и так далее…

Длины отрезков на лучах между точкой А и получающимися точками будут равны последовательным степеням числа х.

Ломаная BCDEFG… может быть продолжена и в другую сторону — по направлению к точке А. В этом случае длины соответствующих отрезков будут давать отрицательные степени числа. Собственно в эту последовательность степеней входит и катет АВ:

Авторами построения были, конечно, не флорентийцы. В их книгах данный метод даже не обосновывался, сопровождаясь традиционной для тех времён ремаркой “с божьей помощью”. :) Да и область применения его довольно ограничена: если число значительно превосходит единицу, то один из углов треугольника становится очень острым, а это на практике неизбежно ведёт к погрешностям.

В наши дни доказать справедливость построения совсем нетрудно в рамках школьной геометрии. Действительно, прямоугольные треугольники АВС и ADC подобны, так как имеют общий острый угол А. Из их подобия следует пропорция

или, в других обозначениях,

откуда и вытекает . Следующие степени получаются применением тех же рассуждений к другим треугольникам.