Метод ложных положений

Обучение алгебре в школе обычно начинается с решения уравнений первой степени (т.е. линейных). Вполне логично: это древнейшее математическое знание, которым человечество владело ещё четыре тысячи лет назад. Но тогда это делалось совсем иначе, нежели сейчас!

Вот, например, задача № 24 из древнеегипетского «папируса Ахмеса», относящегося как раз к упомянутому периоду:

Куча. Её седьмая часть, её целое. Что составляет девятнадцать.

Словом «куча» в египетской математике обозначалась неизвестная величина. Таким образом, эта задача сводится к уравнению

x/7 + x = 19.

Как будет решать его современный школьник? Очевидно, сложит дроби в левой части, приведя уравнение к виду

8x/7 = 19

и затем выполнит действия 19×7/8. Казалось бы, совсем очевидные вещи — чего уж проще?

Однако такой подход основан на двух совсем неочевидных представлениях и умениях:

1. Концепция подобных слагаемых и способность выполнять с ними алгебраические действия;
2. Концепция произвольного представления дробей и способность выполнять с ними арифметические действия.

Что касается первого, то оно было сформулировано лишь во II или III веке нашей эры Диофантом Александрийским — но и тогда это знание сильно опередило своё время. Оно было забыто, в IX веке алгебру переоткрыл аль-Хорезми на персидском Востоке, и только в ХII веке алгебра пришла в Европу… где примерно пять веков считалась «остриём науки» и была доступна лишь избранным из наимудрейших.

Действия же с дробями в привычной нам десятичной системе были разработаны индийцами и пришли в Европу также через персов и арабов, причём примерно в это же время. Словом, египтяне ничего подобного знать в принципе не могли. Для них выражение «целое и его седьмая часть» уже было «каноническим видом», не подлежащим никаким дальнейшим преобразованиям.

А как же они действовали? Тот же папирус Ахмеса свидетельствует, что для решения линейных уравнений применялся так называемый метод ложных положений.

Суть его в том, что берётся произвольное предположение о неизвестной величине и для него считается «отклонение» — разность левой и правой частей уравнения. Современный математик назвал бы эту величину невязкой. Затем бралось второе предположение, для него также считалось отклонение, и по двум этим парам можно было восстановить точное значение неизвестной величины.

Этот приём имел два достоинства. Во-первых, не требовалась никакая работа по преобразованию решаемого уравнения: оно оставалось в своём исходном виде. Во-вторых, для двух предположений можно было (и, собственно, рекомендовалось!) брать такие числа, чтобы предписанные действия производились максимально легко.

Нет ничего удивительного, что метод ложных положений пережил не только египтян, но и Средневековье с Возрождением! Пожалуй, из всех старинных руководств он наиболее вразумительно описан в «Книге абака» Леонардо Пизанского, известного под прозвищем «Фибоначчи». Вот это описание:

Возьми [т.е. представь себе или нарисуй] весы. Над точкою опоры напиши должное число, что получается после действий над искомым. На чаши весов напиши оба предположения. Отклонения с избытком напиши под весами, отклонения с недостатком над весами. Произведи умножение накрест предположений с отклонениями. Результаты возьми разностью, если отклонения записаны по одну сторону, если же по противоположные, то возьми их суммой. Возьми так же и отклонения. Раздели первое на второе.

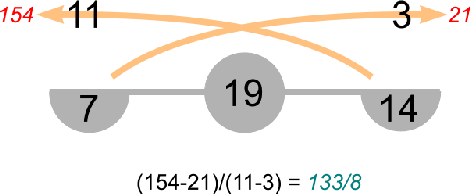
А вот рисунок, иллюстрирующий применения этого метода для египетской задачи:

В качестве предположений здесь берутся числа 7 (отклонение 11) и 14 (отклонение 3), как легко делящиеся на 7. Результат полагалось обязательно проверить подстановкой в уравнение, так как вполне могли получиться «ложные корни»: вычитать полагалось всегда меньшее из большего, так что вполне можно было напутать со знаками.

По египетским понятиям, требовалось ещё привести результат к каноническому виду, которым в данном случае было «шестнадцать с половиной и с восьмой частью».

Осталось только сказать, что в знаменитой «Арифметике» Леонтия Магницкого этот метод назывался «фальшивым правилом».